Perché la significatività statistica è importante?
Scopri perché la significatività statistica è fondamentale nell'analisi dei dati, nella ricerca e nelle decisioni aziendali. Approfondisci p-value, test d'ipote...
Scopri come la significatività statistica determina se i risultati sono reali o dovuti al caso. Comprendi p-value, test delle ipotesi e applicazioni pratiche per la tua azienda nel 2025.
La significatività statistica viene utilizzata per determinare se un risultato è dovuto al caso o causato da un fattore di interesse. Se è statisticamente significativo, è improbabile che sia avvenuto per caso.
La significatività statistica è un concetto fondamentale nell’analisi dei dati che ti aiuta a distinguere tra effetti reali e fluttuazioni casuali nei tuoi dati. Quando conduci esperimenti, sondaggi o analizzi metriche aziendali, hai bisogno di un metodo affidabile per determinare se i modelli osservati sono reali o semplicemente il risultato del caso. La significatività statistica fornisce questo quadro critico utilizzando principi matematici per valutare la probabilità che i risultati osservati si verifichino se davvero non ci fosse alcun effetto o differenza tra i gruppi che stai confrontando.
Il concetto è nato dal lavoro dello statistico Ronald Fisher nei primi anni del XX secolo ed è diventato il pilastro dei test delle ipotesi in praticamente ogni campo che si basa sull’analisi dei dati. Dalla ricerca farmaceutica che convalida nuovi trattamenti fino alle aziende di e-commerce che ottimizzano i tassi di conversione, la significatività statistica fa da spartiacque tra insight azionabili e conclusioni fuorvianti. Comprendere come funziona la significatività statistica ti consente di prendere decisioni informate supportate da solide evidenze piuttosto che da intuizioni o coincidenze.
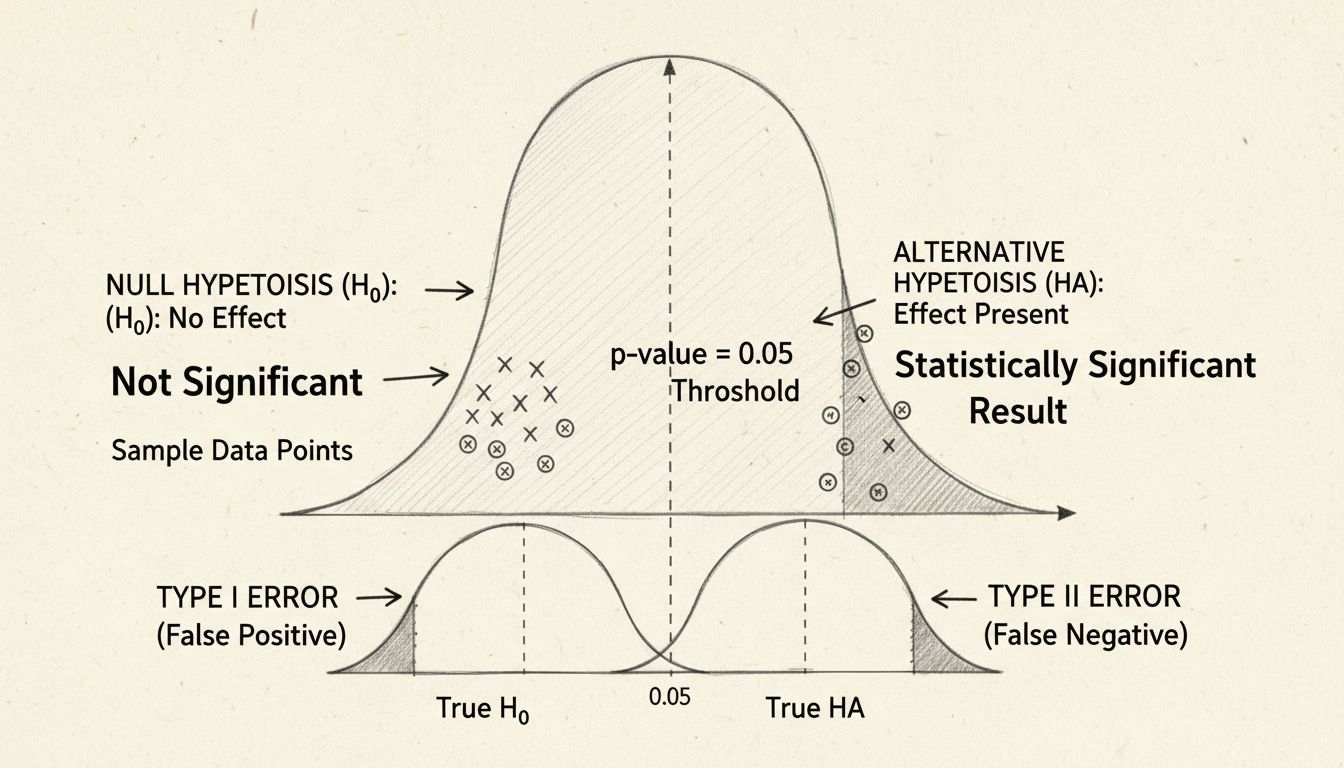
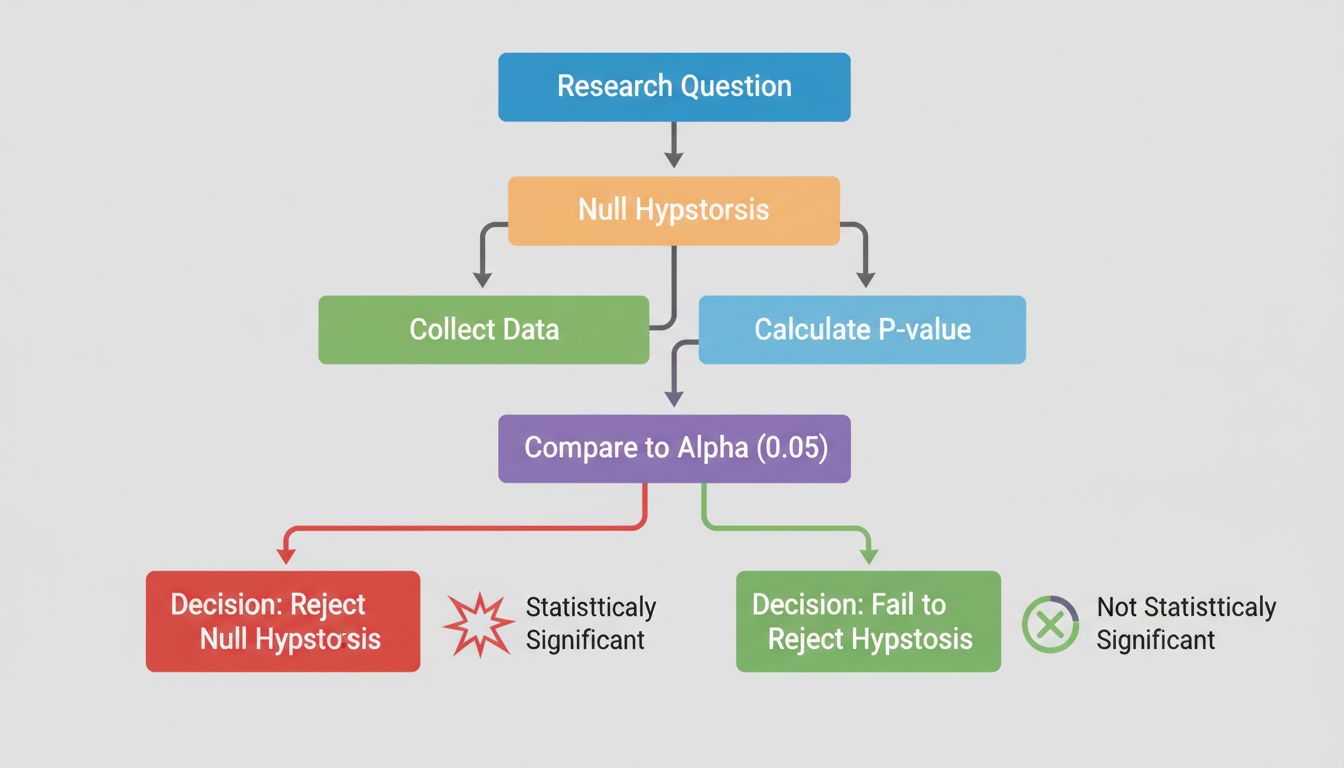
Al centro della significatività statistica si trova il test delle ipotesi, una metodologia strutturata per valutare affermazioni sui tuoi dati. Il processo inizia con la formulazione di due ipotesi contrapposte: la ipotesi nulla e l’ipotesi alternativa. L’ipotesi nulla presume che non ci sia alcun effetto reale o differenza tra i gruppi che stai studiando—in sostanza, rappresenta lo status quo o l’assunzione che ogni differenza osservata sia dovuta esclusivamente al caso. L’ipotesi alternativa, invece, propone che esista davvero un effetto o una differenza.
Considera un esempio pratico: stai testando se una nuova campagna di marketing di affiliazione genera tassi di conversione più alti rispetto al tuo approccio attuale. La tua ipotesi nulla affermerebbe che entrambe le campagne producono tassi di conversione identici, mentre l’ipotesi alternativa sosterrebbe che la nuova campagna si comporta diversamente. Il test statistico valuta quindi quale ipotesi sia maggiormente supportata dai dati. Questo quadro impedisce a ricercatori e analisti di selezionare solo i risultati che confermano le loro aspettative; invece, richiede di dimostrare che i risultati osservati sono improbabili se frutto del solo caso.
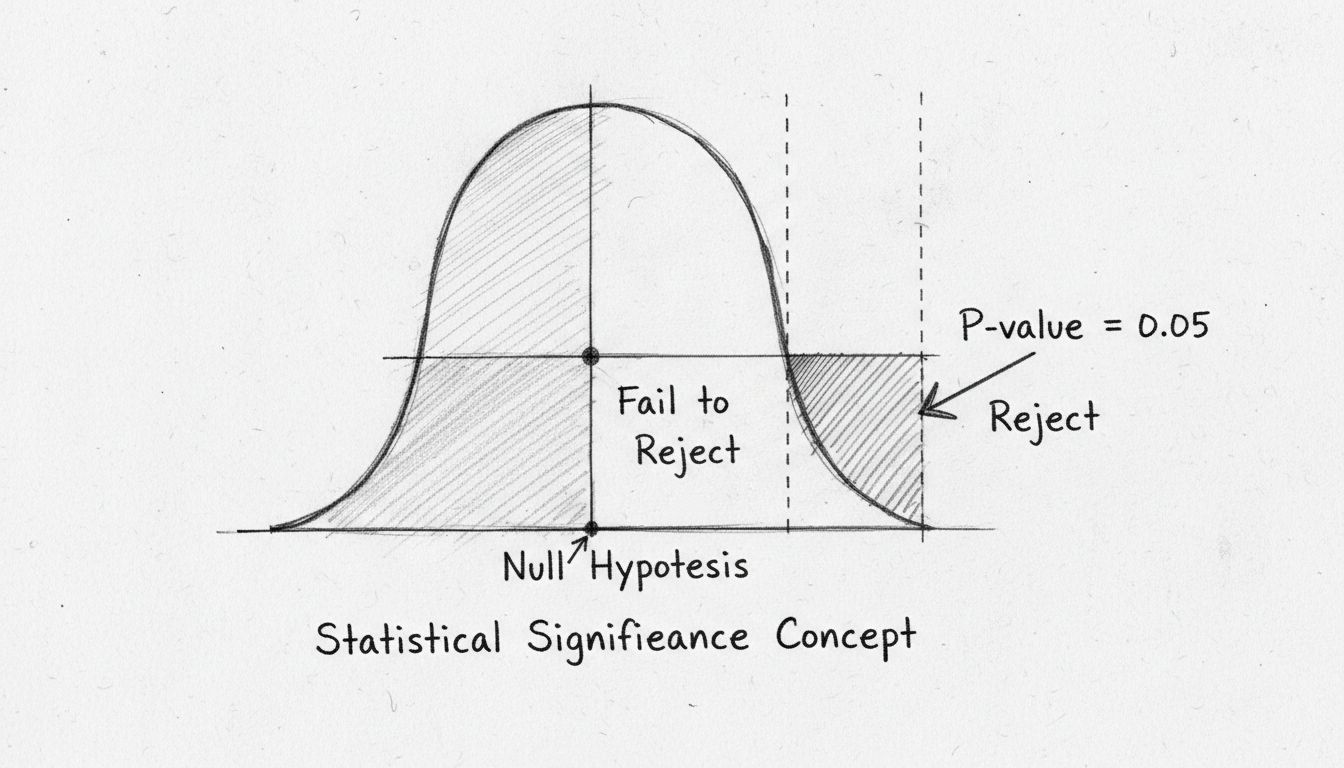
Il bello del test delle ipotesi è la sua oggettività. Invece di affidarsi a giudizi soggettivi, utilizzi calcoli matematici per determinare se i dati forniscono prove sufficienti per rifiutare l’ipotesi nulla. Se le prove sono abbastanza forti, puoi affermare con sicurezza che l’effetto osservato è statisticamente significativo—cioè, è improbabile che sia un caso.
Il p-value è forse la misura più utilizzata nei test di significatività statistica, ma spesso è frainteso. Il p-value rappresenta la probabilità di osservare i tuoi risultati (o risultati ancora più estremi) se l’ipotesi nulla fosse effettivamente vera. In altre parole, risponde alla domanda: “Quanto è probabile osservare questi dati se davvero non ci fosse alcun effetto?” Un p-value basso indica che i risultati osservati sarebbero molto improbabili sotto l’ipotesi nulla, suggerendo che quest’ultima è probabilmente falsa e che l’effetto è reale.
La soglia convenzionale per la significatività statistica è un p-value pari o inferiore a 0,05, che corrisponde a una probabilità del 5% che i risultati siano avvenuti per caso. Questo significa che sei disposto ad accettare un rischio del 5% di rifiutare erroneamente l’ipotesi nulla quando in realtà è vera (chiamato errore di Tipo I). Tuttavia, questa soglia è alquanto arbitraria e varia a seconda del campo e del contesto. Nella ricerca medica, dove le conseguenze dei falsi positivi possono essere gravi, spesso si utilizza una soglia più stringente di 0,01 (1%). Al contrario, in ricerche esplorative o test preliminari, può essere accettabile una soglia di 0,10 (10%).
| Intervallo P-value | Interpretazione | Azione tipica |
|---|---|---|
| p < 0,01 | Altamente significativo | Forte evidenza contro l’ipotesi nulla |
| 0,01 ≤ p < 0,05 | Significativo | Moderata evidenza contro l’ipotesi nulla |
| 0,05 ≤ p < 0,10 | Marginalmente significativo | Debole evidenza contro l’ipotesi nulla |
| p ≥ 0,10 | Non significativo | Evidenza insufficiente per rifiutare l’ipotesi nulla |
È fondamentale capire cosa non indica un p-value. Un p-value di 0,03 non significa che c’è una probabilità del 97% che la tua ipotesi sia vera. Inoltre, non misura la dimensione o l’importanza pratica dell’effetto. Un risultato statisticamente significativo può comunque rappresentare un effetto trascurabile dal punto di vista pratico. Questa distinzione tra significatività statistica e significatività pratica è una delle fonti di confusione più comuni nell’analisi dei dati.
Mentre i p-value ti dicono se esiste un effetto, gli intervalli di confidenza forniscono informazioni cruciali sull’entità e la precisione di quell’effetto. Un intervallo di confidenza è un intervallo di valori che probabilmente contiene la vera dimensione dell’effetto, calcolato con un certo livello di confidenza (tipicamente 95%). Se stai testando se una nuova funzionalità del programma di affiliazione aumenta le commissioni, un intervallo di confidenza al 95% potrebbe indicare che l’aumento reale è compreso tra il 2% e l'8%, con il 95% di confidenza che il valore vero sia in quell’intervallo.
Gli intervalli di confidenza offrono diversi vantaggi rispetto ai soli p-value. In primo luogo, comunicano sia la direzione sia l’entità di un effetto, fornendo un quadro più completo dei risultati. In secondo luogo, aiutano a valutare la significatività pratica—anche se un effetto è statisticamente significativo, se l’intervallo di confidenza mostra un effetto trascurabile, potrebbe non valere la pena implementarlo. In terzo luogo, intervalli di confidenza stretti indicano stime precise, mentre intervalli ampi suggeriscono maggiore incertezza nei risultati.
La dimensione dell’effetto misura la forza della relazione tra variabili o l’entità della differenza tra gruppi. Misure comuni della dimensione dell’effetto includono il d di Cohen (per confrontare medie), coefficienti di correlazione e odds ratio. Un effetto può essere statisticamente significativo ma avere una dimensione dell’effetto ridotta, ovvero un impatto pratico minimo. Al contrario, una grande dimensione dell’effetto potrebbe non raggiungere la significatività statistica se il campione è troppo piccolo. Gli analisti professionisti riportano sempre le dimensioni dell’effetto accanto ai p-value per fornire un quadro completo dei risultati.
La dimensione del campione gioca un ruolo cruciale nel determinare la significatività statistica. Campioni più grandi forniscono più informazioni sulla popolazione e riducono l’impatto delle variazioni casuali, facilitando l’individuazione di effetti reali. Al contrario, campioni piccoli sono più suscettibili a fluttuazioni casuali, che possono portare sia a falsi positivi (individuare un effetto che non esiste) sia a falsi negativi (non individuare un effetto che esiste).
La relazione tra dimensione del campione e potenza statistica è fondamentale nella progettazione della ricerca. La potenza statistica è la probabilità di rifiutare correttamente l’ipotesi nulla quando essa è effettivamente falsa—cioè, la tua capacità di individuare un effetto reale. La maggior parte dei ricercatori mira a una potenza di 0,80 (80%), accettando quindi un 20% di possibilità di non individuare un effetto reale. Per ottenere questo livello di potenza, serve un campione sufficientemente grande, che dipende dall’entità dell’effetto atteso, dal livello di significatività scelto e dal tipo di test statistico utilizzato.
Prima di condurre qualsiasi studio o esperimento, i ricercatori dovrebbero eseguire un’analisi della potenza per determinare la dimensione campionaria richiesta. Ciò evita di sprecare risorse in studi troppo piccoli per individuare effetti significativi e, allo stesso tempo, impedisce studi inutilmente grandi che consumano tempo e denaro. Nel contesto del marketing di affiliazione, significa determinare quanti clic o conversioni bisogna osservare prima di poter concludere con sicurezza che una modifica della campagna abbia avuto un impatto reale.
Domande di ricerca e tipi di dati diversi richiedono test statistici diversi. La scelta del test dipende da fattori come il numero di gruppi da confrontare, se i dati sono distribuiti normalmente, se i campioni sono indipendenti o appaiati e dal tipo di variabile di esito (continua, categorica, ecc.).
Il t-test di Student confronta le medie di due gruppi ed è uno dei test più utilizzati. È appropriato quando hai dati continui (come importi di fatturato) e vuoi determinare se due gruppi differiscono in modo significativo. Il test tiene conto della variabilità all’interno di ciascun gruppo e delle dimensioni campionarie, producendo una statistica t che viene confrontata con un valore critico per determinarne la significatività.
Il test chi-quadrato viene utilizzato per dati categorici per determinare se le frequenze osservate differiscono in modo significativo da quelle attese. Se stai analizzando se il canale di affiliazione (email, social, display ad) influisce sui tassi di conversione, il test chi-quadrato sarebbe appropriato.
L’ANOVA (Analisi della Varianza) estende il t-test per confrontare le medie di tre o più gruppi simultaneamente. Questo previene il problema dei confronti multipli, in cui l’esecuzione di molti test separati aumenta la probabilità di falsi positivi.
Il Mann-Whitney U test e il Wilcoxon rank-sum test sono alternative non parametriche utilizzate quando i dati non soddisfano le assunzioni dei test parametrici, ad esempio quando i dati non sono distribuiti normalmente.
Nel mondo del business, la significatività statistica guida decisioni critiche in numerose funzioni. I team marketing utilizzano l’A/B testing con significatività statistica per determinare se modifiche al sito web, oggetti delle email o creatività pubblicitarie migliorano realmente le metriche di performance. Invece di affidarsi a sensazioni o osservazioni su piccoli campioni, le aziende data-driven stabiliscono soglie di significatività prima di eseguire i test, assicurando che le decisioni siano basate su prove affidabili.
Nel marketing di affiliazione in particolare, la significatività statistica ti aiuta a identificare quali affiliati, campagne e strategie promozionali generano davvero ricavi rispetto a quelli che sembrano avere successo solo per variazioni casuali. Quando valuti se una nuova struttura di commissioni incrementa la performance degli affiliati, il test statistico ti impedisce di apportare modifiche costose basandoti su fluttuazioni di breve periodo. La piattaforma avanzata di analytics di PostAffiliatePro ti permette di monitorare le metriche degli affiliati con il rigore statistico necessario per prendere decisioni di ottimizzazione sicure.
Nella ricerca farmaceutica e medica, la significatività statistica determina se i nuovi trattamenti sono abbastanza efficaci da giustificarne approvazione e utilizzo. Gli studi clinici devono dimostrare che i benefici di un farmaco sono statisticamente significativi prima che possa essere prescritto ai pazienti. Le poste in gioco sono alte, motivo per cui la ricerca medica utilizza tipicamente livelli di significatività più stringenti rispetto ad altri campi.
Uno dei fraintendimenti più diffusi è che la significatività statistica provi la causalità. Una correlazione statisticamente significativa tra due variabili non significa che una causi l’altra. Il classico esempio è la forte correlazione tra l’uscita di film con Nicolas Cage e gli annegamenti in piscina—chiaramente uno non causa l’altro. La significatività statistica indica solo che una relazione è improbabile sia dovuta al caso; provare la causalità richiede prove aggiuntive, come un meccanismo logico, l’ordine temporale e esperimenti controllati.
Un altro errore comune è il p-hacking o data dredging, dove i ricercatori eseguono numerosi test statistici sullo stesso set di dati finché non trovano risultati significativi. Questa pratica aumenta artificialmente la probabilità di falsi positivi, perché con abbastanza test si troverà qualcosa di significativo solo per caso. Se esegui 20 test indipendenti con un livello di significatività di 0,05, ci si aspetta di trovare circa un risultato falso positivo solo per caso. I ricercatori responsabili predefiniscono ipotesi e test statistici prima di analizzare i dati, prevenendo questo problema.
Anche interpretare erroneamente i risultati non significativi è un’insidia. Un risultato non significativo non prova che non esista un effetto; significa solo che non hai prove sufficienti per rifiutare l’ipotesi nulla. Ciò può essere dovuto a campioni troppo piccoli, alta variabilità nei dati o un effetto realmente assente. L’assenza di evidenza non è evidenza di assenza.
La statistica continua a evolversi, con una crescente consapevolezza dei limiti degli approcci tradizionali basati solo sul p-value. Molti statistici ora promuovono un approccio più sfumato che combina p-value con dimensioni dell’effetto, intervalli di confidenza e metodi bayesiani. La statistica bayesiana, che incorpora conoscenze pregresse e aggiorna le convinzioni in base ai dati osservati, offre una cornice alternativa che alcuni ricercatori trovano più intuitiva e flessibile rispetto agli approcci frequentisti.
Il testing sequenziale e i disegni adattivi sono diventati sempre più diffusi, permettendo ai ricercatori di monitorare i risultati man mano che si accumulano i dati e prendere decisioni su proseguire, modificare o interrompere gli studi sulla base di analisi intermedie. Questo approccio è particolarmente utile in ambito business, dove le decisioni devono essere prese rapidamente. Strumenti come Statsig’s Stats Engine implementano il testing sequenziale con controllo del tasso di falsi positivi, permettendo decisioni più rapide e accurate durante gli esperimenti.
La crisi della replicazione nella scienza ha inoltre evidenziato l’importanza di comprendere correttamente la significatività statistica. Molti risultati pubblicati non vengono replicati, in parte perché ricercatori e riviste si sono concentrati eccessivamente sul raggiungimento della significatività statistica, trascurando la dimensione dell’effetto e la significatività pratica. In futuro, l’enfasi sarà posta su trasparenza, preregistrazione degli studi e pubblicazione di tutti i risultati, indipendentemente dalla significatività.
Per usare efficacemente la significatività statistica, stabilisci il livello di significatività e i requisiti di dimensione campionaria prima dell’analisi. Questo previene la tentazione di modificare le soglie dopo aver visto i risultati. Riporta sempre le dimensioni dell’effetto e gli intervalli di confidenza insieme ai p-value per fornire un quadro completo dei risultati. Valuta la significatività pratica dei tuoi risultati—un effetto statisticamente significativo potrebbe essere troppo piccolo per avere un reale impatto.
Sii trasparente sulla metodologia, incluso come hai gestito dati mancanti, outlier e confronti multipli. Se hai eseguito test multipli, applica correzioni appropriate come la correzione di Bonferroni per mantenere il livello di significatività complessivo. Documenta il processo di analisi e sii pronto a condividere dati e codice per la verifica e la replicazione.
Infine, ricorda che la significatività statistica è uno strumento, non una destinazione. Ti aiuta a prendere decisioni migliori riducendo l’influenza del caso, ma va combinata con competenze di dominio, considerazioni pratiche e giudizio aziendale. Nel marketing di affiliazione, la significatività statistica ti aiuta a individuare quali strategie migliorano realmente la performance, ma dovresti anche valutare fattori come i costi di implementazione, la soddisfazione degli affiliati e la sostenibilità a lungo termine quando prendi decisioni strategiche.
Le avanzate analisi e strumenti di reportistica di PostAffiliatePro ti aiutano a monitorare le performance degli affiliati con rigore statistico. Comprendi quali campagne generano realmente risultati e ottimizza il tuo programma di affiliazione basandoti su dati affidabili.

Scopri perché la significatività statistica è fondamentale nell'analisi dei dati, nella ricerca e nelle decisioni aziendali. Approfondisci p-value, test d'ipote...
La significatività statistica esprime l’affidabilità dei dati misurati, aiutando le aziende a distinguere gli effetti reali dal caso e a prendere decisioni info...
Padroneggia significatività statistica test A/B per betting: p-value, confidenza, campioni e ottimizzazione conversioni.
Consenso Cookie
Usiamo i cookie per migliorare la tua esperienza di navigazione e analizzare il nostro traffico. See our privacy policy.